「なぜ?」が分かれば式が立つ!GHSの「体系物理」とは
GHS物理の勉強法の中身とは
これからGHS物理の中身について解説していきますが、あらかじめその中身を一言で述べておきます。GHSの物理の中身とは、
「なぜ」がわかるから式が立つ
ということです。これだけでは、「当たり前では?」と思われるかもしれませんし、そう思うのはむしろ当然です。ですので、百聞は一見に如かず。具体的な問題を例にして説明します。
まずはこの問題を見てください。この問題は、物理の受験生ならだれもが知っている有名な参考書です(余裕がある人は解いてみてください。そうすることでより考え方の違いがはっきりします)。

問題の難易度は標準的です。では、この問題を収録した問題集の解答・解説を見てみましょう。




大事なのは「問題→式」
受験生の皆さんには見慣れた解説でしょうか。ここでこの解説を取り上げたのは、この解説の物理的な不備を指摘するためではありません。答えを出すために必要な式はそろっていますから、「式→答えの解説」としては完璧です。
今回焦点を当てたいのはその「式→答え」の部分ではなく、「答えに至る式は問題文からどうやって出てきたのか?」という「問題→式」の点です。
式から答えを出す計算能力があっても、そもそも問題文から式を立てられなくては計算のしようがありません。
「問題を読んで式を立てられるか」ここが受験生にとって最も大事です。
「問題→式」の流れを見てみよう
この問題のテーマは熱力学という分野に属しますから説明も熱力学に絞って取り上げていきます。
まずは、ピストンの上に重りを乗せた操作について問われています。解答では、初めに、ピストンにかかる力のつり合いにより容器内部の気体の圧力を出しています。この作業は熱力学ではなく、力学に属しますので、今回は取り上げません。とりあえず、気体の圧力は

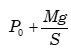
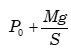
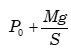
として出たものとして考えていきます。また、この問題ではこれ以降も気体の圧力が変化していきますが、以下、気体の内部の圧力は出せるものとして扱います。
つぎに、おもりをのせる前と後について式を立てています。解答では、「高さh0とh1の状態でボイル・シャルルの法則が成立するから」という前置きでボイル・シャルルの法則を用いて




という式を立てています。
受験生がぶつかる大きな壁 "「なぜ」が分からないと応用ができない"
ここで、物理の実力をつけようとしてこの参考書に取り組んでいる受験生にとって一つの大きな壁が生じます。
「この問題でボイル・シャルルを使うことはわかったが(そう書いてあったが)、他のどの問題にボイル・シャルルを使うのかはわからない」
という壁です。
端的に言うならば、参考書の解説は「式を自力で立てるための解説」にはなっていません(これは参考書・問題集の不備ではありません。もし問題すべてにそうした解説をつけるとなると膨大な労力とページ数がかかります)。
もし、この解説を読んだ受験生がボイル・シャルルの法則が不成立の問題(当然存在します)に当たったとき、一体どうするのでしょうか?
「なぜ」ボイル・シャルルの法則を用いるのか、用いることができるのか、これがわかっていない限り、他の問題にこの法則を適用していくことはできません。
受験生の間で、物理で得意、不得意の差が埋まらない原因はここにあります。
物理の成績を何とかしようと努力する人は、この「なぜ」を知らないまま、問題意識を持たないまま参考書に取り組んでいくので、「物理ができるようになるためにはとにかく問題をたくさん覚えて、パターンを増やすしかない」と思い込んでしまい、やみくもに問題演習を重ねていき、ますます「わからない」勉強へ進んでいくという負の連鎖に陥ってしまいます。
すこし話が飛躍してしまいましたが、ボイル・シャルルの法則に戻りましょう。ボイル・シャルルの法則の成立に必要な条件は
「その変化が閉鎖系で起こっていること」つまり、粒子が容器の中に閉じ込められていて、外に逃げていかないということが成立条件です。このとき、体積・圧力・温度についての式が成り立つので




という式が成り立つのです。
GHSの解法「前後の粒子数は同じ!」

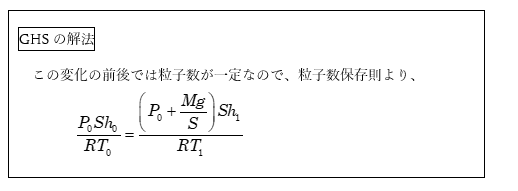


式の形としては気体定数Rがついただけです。しかし、この裏にある「なぜ」には大きな違いがあります。気体の状態方程式
から、
が気体の物質量molを表す量だということは、物理・化学を学んだ人であればわかるはずです。
物質量molとは、平たく言えば「粒子数」です。一粒、二粒・・・と同じと考えてよいでしょう。
GHSでは熱力学を教える際に、「まずシリンダーの中の粒子をイメージする」と教えます。絵で描くと、例えばピストンに重りを乗せたとき、変化の前後で

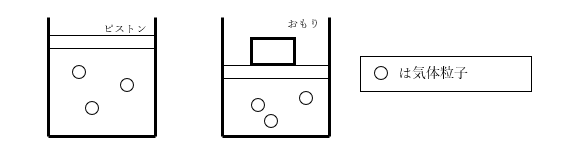


という絵になります。そうすると、変化の前後で粒の数が同じこと、三粒=三粒であることが一目瞭然です。この三粒=三粒という誰でもわかる当たり前の式は、気体の物質量をnmolとすると、nmol=nmolという、これまたごくごく当たり前の式になります。このnmol=nmolを変化の前後の体積・温度・圧力で表現してやれば

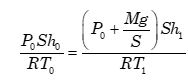
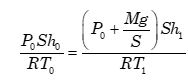
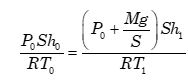
という式が当たり前に出てきます。この「粒子数保存則」が「なぜ」成り立つのか?とGHS生に聞いてみたら
「粒子の数が一定だからですよね?」
と当たり前に返ってきます。
イメージを描いて、イメージ通りに式が立っているのです。
「なぜ」がわかっているのです。
「なぜ」が分かれば一網打尽!
この「なぜ」がわかっていれば、その「なぜ」をこの問題の中でも応用することができます。もう一度同じ問題を見てみましょう。この気体は(1)から(5)までどう変化しているでしょうか?






まず①初期状態があり、②重りが乗せられ、③断熱材を取り外し(これで温度が室温と同じになります)④断熱材を再び取り付け、重りを取り去った(これで圧力がP0へ変化します)という4つの状態になっています。これらすべての変化の中で、粒子数保存則が成り立ちますから、①②③④の状態について

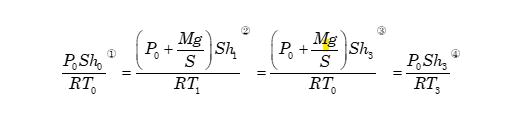
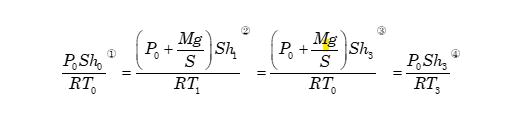
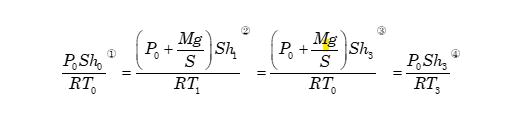
という一つの大きな等式が成り立ち、
あとはこの等式から、問題で問われている答えを出してやればよいだけです。
この問題では、この式から(1)(3)(5)が一つの式で解けます。
(2)(4)についても式から判断することが出来ます。
また、すこし発展した話になりますが、こうして変化の全体像を把握し、それを状態量で表すことには、ここでは書ききれないほどの大きな利点があります。
一例をあげるならば、GHS生は授業で「温度・体積・圧力がわかればどんな問題でも解ける」ということを知っています。
今回は粒子数保存則によって、この変化の中での「体積・圧力・温度」が全てわかりましたね。
そうすると、この次に問われるであろうエネルギー・仕事についても、実は計算が(原理的に)可能であるということがすでに分かって、「これでこの問題は満点がとれたな」という安心感を持ちながら問題を解いていけるのです。
これがどれほど試験に良い影響を及ぼすのかは説明するまでもないでしょう。
さらに、この考え方は他の問題にも応用していくことができます。以下のリンクから、続きを読むことができます。






